In the previous post we described the photographer analogy to explain in a informal way how causal inference works. Now we’ll dive in the theory behind it to understand, in the point of view of structural causal model, what necessary adjustments observational data requires and how they can be performed. But, first we need to defined what is a SCM.
Structural Causal Model and DAGs
A structural causal model consists of set of variables, and a set of functions that assigns each variable a value based on the values of the other variables in the model. Such functions represent the causation between variables: A variable X is a direct cause of a variable Y if X appears in the function that assigns Y’s value. X is a indirect cause of Y, if it is appears in any function, indepedent of the depth, of the variables that are inputs of f which defines the value of Y.
X is a direct cause of Y: Y = f(X, Other Variables)
X is an indirect cause of Y: Y = f(Z, Other Variables) and Z = g(X, Other Variables)
Every SCM is associated with a graphical causal model that is represented as a DAG (directed acyclic graph). “DAGs consist of three elements: variables (nodes, vertices), arrows (edges), and missing arrows. Arrows represent possible direct causal effects between pairs of variables and order the variables in time. The arrow between C and Y means that C may exert a direct causal effect on Y for at least one member of the population. Missing arrows represent the strong assumption of no direct causal effect between two variables for every member of the population (a so-called “strong null” hypothesis of no effect). The missing arrow between T and Y asserts the complete absence of a direct causal effect of T on Y. DAGs are nonparametric constructs: They make no statement about the distribution of the variables (e.g., normal, Poisson), the functional form of the direct effects (e.g., linear, nonlinear, stepwise), or the magnitude of the causal effects.” Handbook of Causal Analysis for Social Research, pag. 248.
To make clearer, we can imagine the SCM as the mechanism by which a dataset is generated. So, if we have the full specification of the SCM, all functions and independent variables, we can recreate the associated dataset. In the demonstration post (part 4), we will use a full specified SCM to simulate causal inference studies for the purpose to show how the algorithms perform.
Bringing this definition to the intervention setting, where we want to discover the effect of a treatment, we could draw a generic DAG to help us to visualize and understand what happens in a intervention study. The next figure shows a very simple DAG, where the T variable is the treatment, the O is the outcome yielded after the treatment has been applied and the covariates from V1 to VN represent the influences on the treatment assignment process. From now on, we’ll gonna call all variables different from T and O in a intervention SCM by covariates.
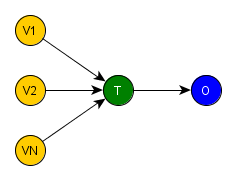
If we remember our previous post, one of the main characteristics of a random experiment is the random assignment of the treatment, i.e. it is influenced by no covariate. Therefore, if we redraw the previous DAG now representing a generic random experiment, we would obtain the figure below, where there is no edge entering T, i.e. T is independent of the covariates V1, …, VN.
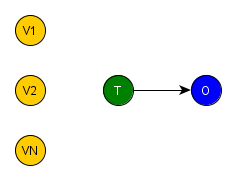
Summing up, these simple DAG’s give us a clear purpose. We need to find a process that performs a blockage of V1, …, VN’s influence over the treatment variable in the observational dataset, which is formally defined ahead by the backdoor criterion. However, to perform causal inference of the treatment effect, we need to keep intact O=fo(T,PAo) after the adjustments, i.e. the causal relation T -> O and PAo -> O, where PAo represents all covariates that have edges entering in O, i.e. the covariates parents of O. But first, we need to understand the basic configurations of covariates connections in a SCM.
Three Possible Causal Configurations of Covariates and Their Blockage Behavior on Conditioning
=> Chains. Rule 1 (Conditional Independence in Chains). Two covariates, A and C, are conditionally independent given B, if there is only one unidirectional path between A and B and C in any set of covariates that intercepts that path. So if you condition on (filter) B, you block the causal link connection B-C.
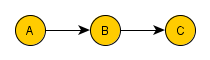
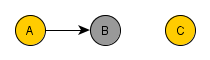
To understand why this happens, we need to remember that when we condition on B, we filter the data into groups based on the value of B, i.e. we create many datasets, each with the same value of B, that together recreates the original one. Now, we select only the dataset where B=b to take a closer look. We want to know whether, in these cases only, the value of C is independent of the value of A. We know that, without the conditioning over B, if the value of A changes the value of B is likely to change. And if the value of B changes, the value of C is likely to change as well. But as we are looking only in the dataset where all values of B is equal b, all values of A in this dataset entails B=b. Therefore, C remains unaltered for any change of A in this dataset. Remember that the same thing applies to all datasets with the same value for B. Thus, C is independent of A, conditional on B.
=> Forks. Rule 2 (Conditional Independence in Forks). If a covariate B is a common cause of covariates A and C, and there is only one path between A and C, then A and C are independent conditional on B. So if you filter B for a specific value, you block the causal link connection B-A and B-C. We can also use the previous rationale to justify this case.
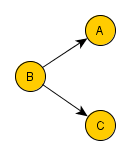
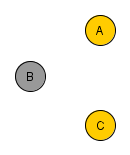
=> Colliders. Rule 3 (Conditional Independence in Colliders) If a covariate B is the collision node between two covariates A and C, and there is only one path between A and C, then A and C are unconditionally independent but are dependent conditional on B and any descendants of B. So if you filter B for a specific value, you block the causal link connection A-B and C-B. However, you create a spurious causal link connecting A and C.
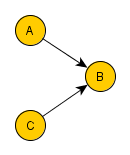
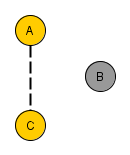
Judea Pearl explains very clearly, in his book – page 41, this apparent strange behavior:
“Why would two independent covariates suddenly become dependent when we condition on their common effect? To answer this question, we return again to the definition of conditioning as filtering by the value of the conditioning covariate. When we condition on B, we limit our comparisons to cases in which B takes the same value. But remember that B depends, for its value, on A and C. So, when comparing cases where B takes, for example, the value b, any change in value of A must be compensated for by a change in the value of C — otherwise, the value of B would change as well.”
These three possible configurations will be the base for the definition of the backdoor criterion in the next section, which states how the adjustment in observational data can be done to simulate a random experimental dataset. If you’d like more details on these configurations, check this post and/or this book out.
General DAG of Intervention Study on Observational Data

When you think about possible kinds of the covariates inside a SCM of a intervention study, we can separate them in 2 groups that are overlapped:
- Based on the time flow:
- Pre-treatment. These are covariates that are not affected by the treatment and their values are defined previous to the execution of the intervention;
- Post-treatment. These are covariates that are affected by the treatment and their values are defined after the intervention is executed.
- Based on measurement:
- Measured and Recorded. These are the covariates that were correctly measured during the study and they will be the base for our adjustments.
- Unmeasured. These covariates are the ones left out of the measurement process and their impact in the causal inference process must be assessed. When a important covariate is ignored, the conclusion drawn after the adjustment is possibly distorted.
The sets contained inside each combination of these two groups must be dealt with in specific ways to properly enable the measurement of the treatment’s impact:
- Measured and Recorded / Pre-Treatment: All covariates contained by sets 1,2 must satisfy the backdoor criterion relative to variables T and O, i.e. we need to block their influence on the treatment variable. As these sets are composed by covariates that fits the configuration represented by chains and forks, it is possible to use conditioning on them, creating a blockage without spurious paths appearing on the covariate previously connect to the treatment variable;
- Unmeasured / Pre-Treatment: Sets 4,5 must be empty, once they contain only unmeasured covariates. Otherwise, they won’t satisfy the backdoor criterion. Thus, we need to use theory or empirical knowledge of the domain in question to state a justification that both sets are empty;
- Measured and Recorded / Post-treatment: All covariates contained by set 3 must be ignored during the adjustment process. So, we must identify all covariates in set 3 also using theory or empirical knowledge and remove them from the covariates that will participate in the blocking process. If they wrongly participate, we would create spurious paths on the treatment variable as shown in the diagrams explaining the collider connection. Thus, possibly introducing more bias into the dataset;
- Unmeasured / Post-treatment: Finally, set 6 is automatically ignored, once none of its covariates were measured.
Those steps are based on the backdoor criterion, which is stated below:
(The Backdoor Criterion) Given an ordered pair of variables (T, O) in a directed acyclic graph G, a set of covariates satisfies the backdoor criterion relative to (T, O) if no covariate in this set is a descendant of T (i.e. these covariates cannot be contained by sets 3,6), and they BLOCK every path between T and O that contains an arrow into T. In other words, these covariates must be contained by sets 1,2 only. If you’d like more details on that, check this book – page 61.
But how we can block the influence of these covariates? In the previous section, we learnt that is possible to block variables if we use condition probability (filter). This would allows us to use Bayesian statistics to find the equation representing the effects of the treatment after adjusting for sets 1 and 2. However, it is a big problem to use this approach in real data. Judea Pearl in his book – page 72, describes it very precisely:
‘It entails looking at each value or combination of values of [the covariates in sets 1 and 2] separately, estimating the conditional probability of [O] given [T] in that stratum and then averaging the results. As the number of strata increases, adjusting for [sets 1 and 2] will encounter both computational and estimational difficulties.
Since the [sets 1 and 2] can be comprised of dozens of variables, each spanning dozens of discrete values, the summation required by the adjustment formula may be formidable, and the number of data samples falling within each [possible value combination of the covariates in sets 1 and 2’s] cell may be too small to provide reliable estimates of the conditional probabilities involved.’ – The text inside brackets was adapted for clarity.
Now what? Give up? Is there another possible way to apply the backdoor criterion by blocking covariates without applying conditional probability for each one of them?
Propensity Score to The Rescue
The propensity score is the conditional probability of assignment to a treatment group given the covariates. It can be described as a balancing score. This means that, conditional on the propensity score, treatment variable is independent of measured baseline covariates. Therefore, the distribution of all covariates is the same in the treatment group as in the control group.
Now in English: To simplify the explanation, we’ll limit the propensity score in this post series to exactly two levels, as defined by Rosenbaum and Rubin (1983), that roughly translates in the probability of a subject being treated given her background characteristics. So, in an ideal randomized trial, the propensity score is p(T=1)=0.5 for all individuals, independent of the final group (treatment or control) that they were assigned to.
In contrast, in observational studies some individuals may be more likely to receive treatment than others, which creates biases. So, the adjustment that must be applied to this dataset will force the probability of treatment assignment to be set to 0.5, when conditioned on PS: p(T=1|ps(PAt))=0.5, where PAt are all covariates parent of T. But, first we need to know the true propensity score function of the dataset. Unfortunately it is a unknown function, once the treatment assignment is beyond the control of the investigators. Therefore, the only alternative is to estimate it directly from the data using statistical models. Which in turn, creates a new condition that must be satisfied: no model misspecification. In case of misspecification, even if we achieve the final result p(T=1|ps(PAt))=0.5 for all observations, yet the paths between T and covariates in the sets 1 and 2 wouldn’t be completely blocked. It is important to keep in mind, when all paths between T and covariates in the sets 1 and 2 are blocked, it entails that p(T=1|ps(PAt))=0.5, but not the other way around.
Now the problem resumes in studying which techniques are the best to properly estimate the PS function from data. But, for didactical purpose, we’ll skip this step for now and dive in the process of using these estimated treatment assignment probabilities to perform the needed adjustments.
We Have The PS Estimation, Now What?
Estimating the propensity score function using statistical model is only the first task. Now, we need to choose the appropriate approach to balance the distribution of the covariates in sets 1,2 between treatment and the control group. The most commons are:
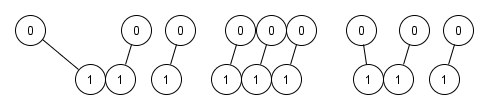
Matching. As the name imply, it matches observations from the treatment with the control group with the closest given a predefined distance function based on the estimated propensity score. Often the group with fewer subjects is the base and the other group is used to find the matches. The base group defines the subpopulation on which the causal effect is being computed, which usually implies in observations being discarded in the other group. Moreover, matching doesn’t need to be one-to-one (matching pairs), as portrait in the figure below, but it can be one-to-many (matching sets). Because the matched population is a subset of the original study population, the distribution of causal effect modifiers in the matched study population will generally differ from that in the original, unmatched study population;
An imaginary propensity score horizontal axis from left to right
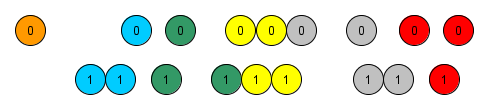
Stratification / restriction. It matches all treatment observations to the control ones inside a stratified propensity score by quantiles or by uniform intervals, in the figure below the stratas are represented by the colors. Given the proportion between control and control observation in each strata, weights are calculated and attributed to the observations in that strata;
Many times one of the groups stands alone in the strata, as represented by the orange one below, and a merge must be performed
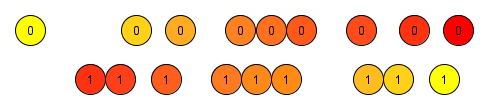
Inverse Probability Weighting. It is a way to correct for the over-representation of certain types of individuals, where the “type” is captured by the probability of being included in the treatment. It uses weights based on the propensity score to create a artificial population in which the distribution of measured covariates is independent of treatment assignment. The use of IPW is similar to the use of survey sampling weights that are used to weight survey samples so that they are representative of specific populations (Morgan & Todd, 2008). The figure below represents the new weights, in colors intensity, based on the propensity score, an imaginary horizontal axis from left to right. We can notice that it creates a symmetry between weights on the treatment and the control group, which reduces the unbalancing. The way the weights are calculated in the IPW technique allows the execution of multiple iterations, where the next always improves on the last one. This characteristic enables a certain tolerance of misspecified treatment assignment probability models, once the next iteration can always try to compensate what the last one misspecified. Which creates a robustness non existent in the previous described techniques. Therefore, IIPW is even able to adjust for a non-linear treatment assignment probability mechanism using a linear treatment assignment probability model (van der Wal, W.M 2011).
Wt=1/ps and Wc=1/(1-ps)
Before we choose our method, we need to explicitly define the causal question to be answered. Otherwise, misunderstandings might easily arise when effect measures obtained via different methods appears to be different. As we want to estimate the mean of the causal function of O for values T=0 and T=1, we don’t need to hold the proportion of the treatment or the control population static. Therefore we can accept the creation of artificial populations based on the initial one. Thus, for this post, we chose IP Weighting (book – Chapter 12), because it is perfect to calculate the causal effect to the entire population and it has an interesting property that allows us to iterate the balancing process.
ATE vs ITE
So far the procedure described has the purpose to estimate ATE = Ê[O|T=1]- Ê[O|T=0] for the population represented by the observational dataset, ATE stands for average treatment estimate, and to check the probability of the null hypothesis violation using a t-test. In resume, it uses a iterative PS function, T=ft(PAt), estimation to reweight the observations, thus creating a final adjusted observational dataset. However, is it possible to use this estimation to calculate the ATE for a different population, i.e. different observational dataset?
Yes! To do that we need to estimate, from the adjusted data, the function O=fo(T,PAo), which defines the causal effect of the variable T in the variable O. Using such function, we can estimate the ITE, individual treatment estimation, for each observation in the new dataset and then its ATE, given that we have PAo, the covariates parents of O.
However, a few conditions must be satisfied by the adjusted dataset to allow a correct estimation of O=fo(T,PAo):
- A statistical algorithm that yields KS {fo(T=0,PAo), Ê[O|T=0]} and KS {fo(T=1,PAo), Ê[O|T=1]} very small, where KS is Kolmogorov-Smirnov the test of homogeneity, after the adjustment;
- And finally, the observational data used to estimate the propensity score must have a minimum number of observations to properly estimate the distribution of the covariates.
The estimation of fo(T,PAo) is a regular machine learning prediction procedure, where we need to split the adjusted observational data in training, validation and test dataset and use a machine learning algorithm complex enough to properly fit the data.
Wrapping up
In this post we described how causal reality can be modeled using SCM and how we can use backdoor criterion with propensity score function estimation to remove confounding and selection biases, thus guaranteeing the exchangeability condition. We decided that the best approach to use the estimated treatment assignment probabilities is using IIPW to maximize the chance to avoid the misspecification model problem.
In the next post we’ll return to the point we skipped about the techniques necessaries to estimate PS and describe other practical aspects to implement the desired algorithm for causal inference the best way possible.
Previous Post – Causal Inference Study Motivation: The Photographer Analogy
Any feedback send to frederico.nogueira@gmail.com